2023. 5. 19. 08:50ㆍData science/Machine Learning
Unsupervised or Supervised Classification
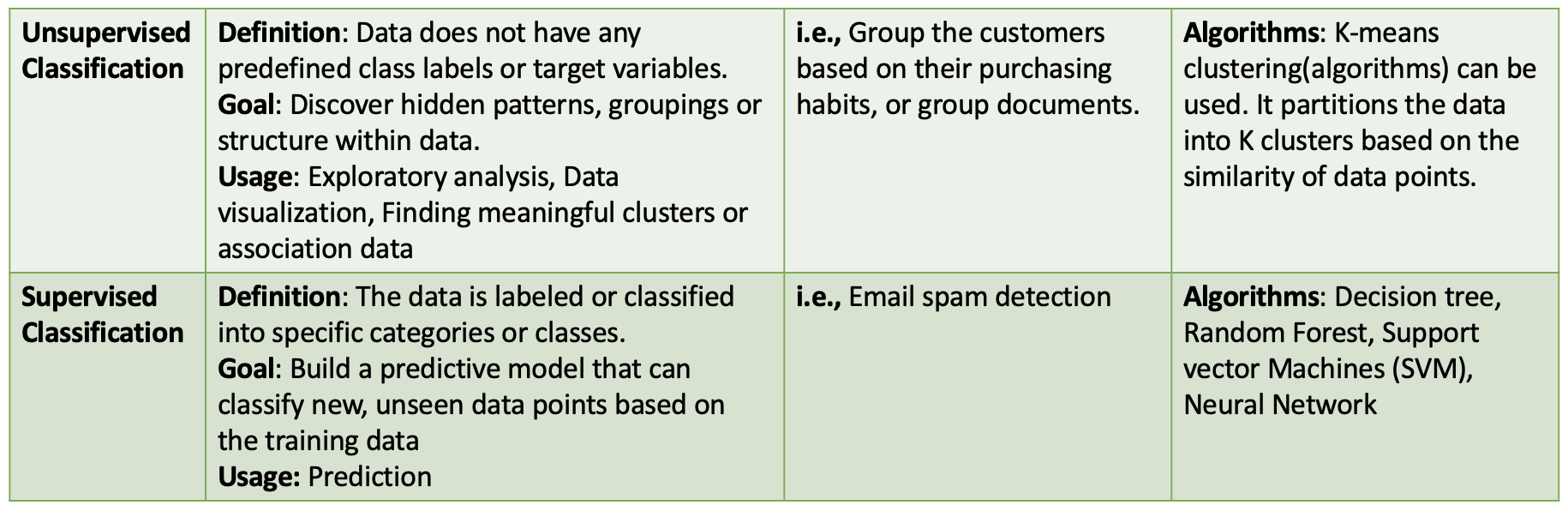
This post will focus on classification algorithms, such as K-means, model-based clustering, K nearest neighbours and probabilistic classifiers.
K-means
K-means clustering is a popular unsupervised machine learning algorithm to partition a dataset into k distinct clusters. It aims to minimize the within-cluster sum of squares by assigning data points to clusters based on their proximity to cluster centres. * distance can be measured by the standard Euclidean distance: d(x_j, x_n) = || x_j - x_k ||₂
-> which makes the total within-cluster sum of squares minimized.
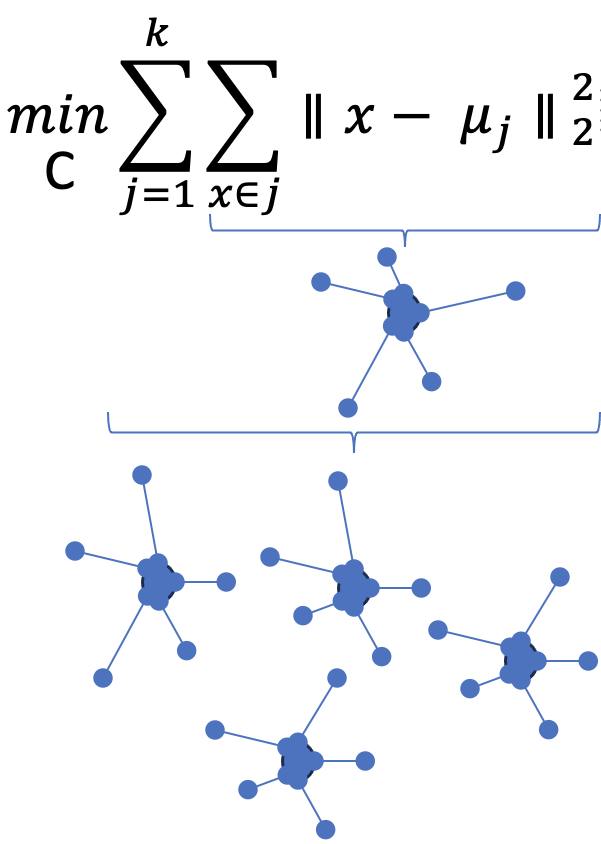
How to do the K-means?
- Initialization: Start by selecting k initial cluster centres. Various methods can be used, such as choosing random points, points from the dataset, or a centrally located point.
- Assignment Step: For each data point, calculate the Euclidean distance to each cluster centre and assign the point to the cluster with the closest centre. The distance can be computed using the standard Euclidean distance formula.
- Update Step: After assigning all points to clusters, update the cluster centres by calculating the mean of the data points within each cluster. The new cluster centre represents the average position of the data points in that cluster.
- Convergence Check: Check if the cluster centres have converged. If the positions of the cluster centres remain unchanged or the change is below a predefined threshold, the algorithm stops. Otherwise, repeat steps 2 and 3.
** Clustering depends on the initial centres. Thus, run the algorithms with different initial centres, then choose the result with the smallest sum of squares.
** To decide how many clusters to keep, using an elbow plot can be helpful. Choose the value of k where the break occurs in the slope.
How to choose centres?
- Random Initialization: Choose k points uniformly and randomly from the data space. This approach is simple and suitable when the data distribution is uniform.
- Forgy's Method: Select k points from the dataset as the initial cluster centres. This method ensures that the initial centres are representative of the data points.
- Random Partition: Assign points to clusters uniformly at random, with each cluster initially having approximately n/k points. Use the cluster means as the initial centres.
- Centrally-Located Point: Choose the most centrally located point in the dataset as the first centre and subsequently select the points with the largest minimum distance to all existing centres.
- Maximin: Begin by selecting a centre arbitrarily and then choose subsequent centres as the data points with the largest minimum distance to all existing centres. This method ensures that the initial centres are well-separated.
Determining the Number of Clusters:
The choice of the number of clusters, k, is crucial. One approach uses an elbow plot, which displays the relationship between the number of clusters and the within-cluster sum of squares. Identify the value of k where the plot shows a significant break or reduction in the slope, indicating a good balance between compactness and separation of clusters.
Model-based clustering; EM algorithms
Model-based clustering is a powerful technique that allows us to discover underlying patterns in data by fitting a probabilistic model to the observed data. The Expectation-Maximization (EM) algorithms are commonly used to estimate the model's parameters in a maximum likelihood framework.
Model-based Clustering involves specifying the number of clusters in advance and then fitting a probabilistic model to the data. A probability distribution represents each cluster, and the goal is to estimate the parameters of these distributions that best explain the data.
EM Algorithms: The EM algorithm is an iterative optimization technique to estimate the model parameters. It consists of two steps- The expectation and Maximization steps.
- Initialization: Start by assigning points to clusters uniformly at random and construct an initial class membership matrix, z, using one-hot encoding.
- Expectation step: Compute the mixture parameters, such as the mixing coefficients (𝛑), mean values (𝛍), and covariance matrices (𝚺), based on the current estimates.
- Maximization step: Update the cluster assignment probabilities using the newly estimated mixture parameters. This involves calculating the probabilities of points belonging to each cluster based on the model's parameters.
- Convergence check: If the cluster assignment probabilities, z_ij, are not changing significantly, stop the algorithm. Otherwise, repeat steps 2 and 3 until convergence is achieved.
Benefits of Model-based Clustering
- Flexibility: Model-based clustering allows for more flexible cluster shapes and can accommodate various types of data distributions.
- Uncertainty Estimation: The algorithm provides probabilities of class membership for each data point, allowing uncertainty quantification.
- Scalability: Model-based clustering can handle large datasets using efficient algorithms and approximation techniques.
Choosing the number of clusters
Selecting the appropriate number of clusters is a crucial step in model-based clustering. BIC or cross-validation can be used to determine the optimal number of clusters that best balance model complexity and goodness of fit to the data.
K-nearest neighbours
K-nearest neighbours (KNN) is a simple yet effective classification algorithm that makes predictions based on the proximity of training data points to a test feature vector.
1) Given a test feature vector x, the KNN algorithm identifies the k nearest neighbours in the training set based on a specified distance metric. The distance metric can be Euclidean distance, Manhattan distance or any other suitable similarity measure.
2) Take a majority vote from those K for the predicted class of the test datapoint ( K should be odd).
KNN offers several advantages, including its simplicity and flexibility. It can handle both classification and regression tasks and adapt to various data types.
** The choice of K: A small value of K may lead to overfitting, while a large value of K may result in underfitting (smooth boundary, but high bias and low variance, reduce noise impact).
** KNN relies on distance calculations; it is crucial to normalize or scale the features to ensure that no single feature dominates the distance calculation. ( z-score normalization or min-max scaling)
** Recommendation systems, image recognition and anomaly detection are useful when the decision boundaries are complex, or the training data is unbalanced.
Probabilistic Classifiers
Probabilistic Classifiers are a class of machine learning algorithms that assign probabilities to different classes or categories for a given input. Instead of providing a single predicted class, probabilistic classifiers estimate the likelihood or probability of an input belonging to each class.
1) Probability estimation: Probabilistic classifiers provide a probability distribution over all possible classes for a given input.
2) Decision boundary separates different classes based on the estimated probabilities.
3) Training process: The algorithm learns the relationship between input features and class labels using a labelled dataset. The process involves estimating the parameters of the probability distribution for each class.
4) Bayesian framework: Often based on the Bayesian framework, which incorporates prior knowledge and updates it with observed data using Bayes' theorem.
5) Evaluation: Evaluated using various metrics such as prolonged loss, accuracy, precision, recall and F1-score.
** Logistic regression, Naive Bayes and support vector machines with probabilistic outputs.
** Spam detection, sentiment analysis, medical diagnosis, and fraud detection
'Data science > Machine Learning' 카테고리의 다른 글
| Markov chain Monte Carlo (0) | 2023.05.20 |
|---|---|
| PCA (Principal Components Analysis) (0) | 2023.05.19 |
| Machine Learning and Stats 2 - Univariate Exploratory Data Analysis (0) | 2023.01.17 |
| [IBM] What is Data Science? - Deep Learning & Machine Learning (0) | 2021.05.15 |